Il 19 agosto scorso una tempesta improvvisa nel Tirreno, vicino Palermo, affonda il Bayesian. È un mega-yacht di 56 metri con a bordo il milionario imprenditore Mike Linch, noto come lo Steve Jobs britannico. La storia, già molto strana, incuriosisce per il nome dello yacht che non è, come è consuetudine, ispirato alla moglie o al cavallo preferito del miliardario.
Il nome della nave affondata deriva invece dalla matematica: il Teorema di Bayes.
Oggi questo teorema è usato per analisi statistica nei campi più svariati, dalla medicina all’intelligenza artificiale. Inizialmente, però, fu usato per un compito ancor più ambizioso: dimostrare l’esistenza di Dio. La nascita e l’evoluzione del teorema dimostrano l’importanza della matematica nella vita di tutti i giorni, e meritano di essere raccontate.
La storia di Mike Linch e del suo software Darktrace
Nel 1990, Mike Linch è uno studente di Cambridge che studia reti neurali. Ha la vocazione dell’imprenditore. Fonda Autonomy, una ditta di software per la ricerca e analisi di informazioni in masse enormi di telefonate, video e email; un motore di ricerca per dati caotici e insicuri in cui usa la matematica di Bayes per trovare, con un certo grado di probabilità, ciò che si vuole. Nel 2011 la multinazionale HP compra Autonomy per 11 miliardi di dollari, rendendo Mike Linch ricchissimo. Fonda altre ditte di successo: Featurespace, per prevedere frodi per banche o società di scommesse; Neurence, che usa machine learning per riconoscere oggetti; e soprattutto Darktrace, un software che si inserisce nella rete dati di una ditta e la analizza.
La maggior parte degli antivirus funziona come il muro di una città medioevale, respingendo eventuali invasori che però, una volta entrati, sono liberi di fare ciò che gli pare; Darktrace è diverso, più simile al nostro sistema immunitario che a un muro, e riesce a individuare comportamenti sospetti anche dentro il network che sorveglia. Se qualche computer della ditta comincia a comportarsi in maniera strana, ad esempio mandando molti email, Darktrace se ne accorge e suona l’allarme. Ci riesce usando la statistica di Bayes.

Il successo rende presto la vita di Mike Linch avventurosa.
La HP gli fa causa per miliardi di dollari, accusandolo di aver gonfiato il valore di Autonomy.
A marzo 2023 Linch è estradato negli Stati Uniti, passa dieci mesi agli arresti domiciliari, poi vince il processo. Per festeggiare la libertà ritrovata, parte per una crociera di lusso in Sicilia, e lì il suo yacht affonda a causa di una tempesta improvvisa, che viene quasi da definire improbabile.
Negli stessi giorni muore anche il vicepresidente di Autonomy, investito da un’auto mentre fa jogging; le due morti così vicine scatenano ogni sorta di teorie cospirative, che includono anche un possibile ruolo di servizi segreti di nazioni interessate ai suoi software.
Una delle voci correnti è che Darktrace sia stato usato per localizzare i leader di Hamas a Gaza, o sabotare sistemi russi a Kursk.
Chissà se Mike Linch sarebbe riuscito a calcolare le probabilità che il suo yacht ultramoderno affondasse in pochi minuti a causa di una tempesta come mai se ne vedono in Sicilia usando la formula del vecchio reverendo Bayes.
La storia del Teorema di Bayes
Nella Londra del ‘700 Thomas Bayes è uno studioso come tanti altri, un pastore presbiteriano che nella sua vita ha pubblicato due libri, uno di teologia e l’altro di statistica, nessuno dei due di grande successo.
Alla sua morte però il suo collega e amico Richard Price trova tra le sue carte un’interessante dimostrazione matematica. Semplificando parecchio, secondo Bayes la probabilità di un evento non è un numero fisso e immutabile, ma varia di continuo alla luce di nuove informazioni. Esempio pratico: oggi potrebbe piovere, e possiamo stimare una certa probabilità per questo evento. Se il cielo è nuvoloso, la probabilità di pioggia aumenta. Conoscendo la probabilità assoluta (cioè a priori) di giorni nuvolosi e giorni di pioggia, il teorema di Bayes calcola la probabilità che piova dopo aver preso ulteriori informazioni, cioè dopo aver visto che il mattino è nuvoloso.
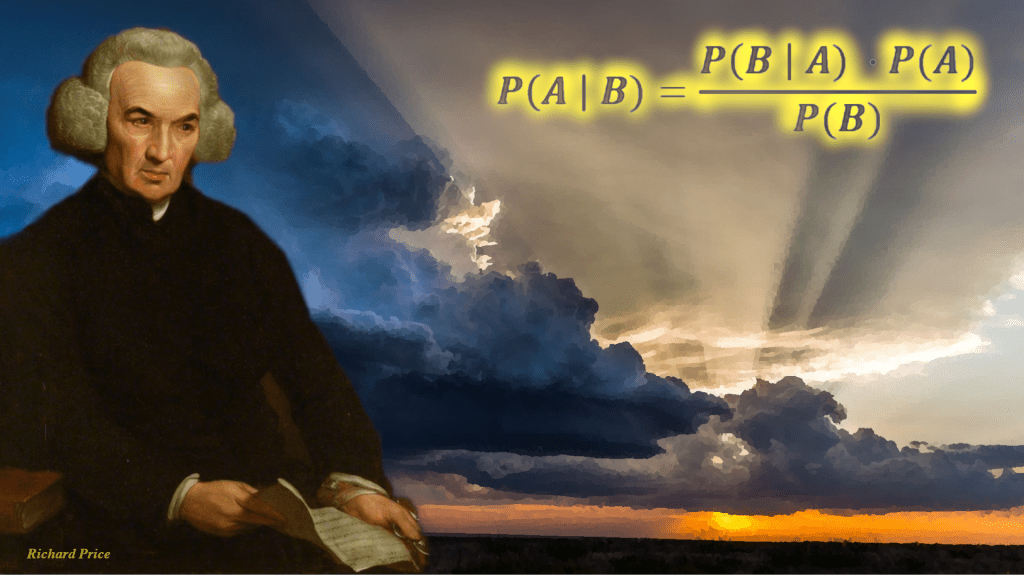
Forse questi ragionamenti vi sembrano cervellotici e astrusi ma la matematica, per quanto indigesta a molti è, citando Galileo, “la lingua con cui Dio ha scritto l’Universo, e chi non la conosce si aggira in un oscuro labirinto”. Le formule matematiche, per quanto astratte, possono agire prepotentemente nel mondo reale, e la formula di Bayes lo dimostra in varie occasioni, nei secoli successivi.
Price, oltre che pastore anglicano è anche un matematico e vede nel teorema di Bayes un’arma per vincere una discussione religiosa.
Da poco il filosofo David Hume ha infatti messo in dubbio l’esistenza dei miracoli. “Se qualcuno mi dice che è successo un miracolo” scrive Hume “è più probabile che le leggi della natura siano cambiate, anche solo per un attimo, oppure che l’uomo stia mentendo? Sicuramente la seconda, visto che le leggi della natura sembrano immutabili: ad esempio il sole sorge sempre ogni giorno, e la marea arriva puntuale”. Quindi Hume suggerisce che i miracoli siano tutti bugie.
Price usa il neonato teorema di Bayes per dimostrare che c’è una probabilità , seppur minima, che le leggi della Natura possano cambiare; ad esempio, che la prossima marea non arrivi, anche se l’abbiamo vista arrivare migliaia di volte. Price stima quella probabilità pari, come minimo, ad una su tre milioni. Molto bassa ma non nulla. Il ragionamento sembrerà strano, ma all’epoca la fede religiosa e l’esistenza di Dio sono un punto fermo per tutti, anche e soprattutto per gli scienziati; infatti Hume accetta il ragionamento come “possibile e ingegnoso, e forse anche solido”.
Nei secoli successivi il teorema di Bayes diventa ben noto a tutti gli esperti, ma rimane poco usato, più che altro è una curiosità. Nel 1950 questo modo di interpretare la probabilità basato su ipotesi invece che su numeri assoluti è chiamato Statistica Bayesiana.
La statistica Bayesiana comincia ad essere applicata nei campi più svariati, informatica, test medici, previsioni economiche… è particolarmente adatta per affrontare situazioni caratterizzate da alta incertezza, dove le informazioni sono limitate e soggette a cambiamenti rapidi.
Poi arrivano i computer che permettono di modellare l’evoluzione di sistemi complessi, risolvendo problemi anche dove non è possibile calcolare una precisa soluzione matematica. Poi arriva la rivoluzione dell’intelligenza artificiale e l’applicazione della statistica Bayesiana riceve un’ulteriore accelerazione. Gli smartphone, per indovinare la parola successiva che vogliamo scrivere in un messaggio, usano statistica Bayesiana aggiornando la probabilità di ogni parola man mano che imparano il nostro stile.
Il teorema di Bayes aiuta a rivelare alcuni casi, anche ingannevoli, di statistica.
Esempio pratico di applicazione del Teorema di Bayes
Immaginiamo di vedere un uomo in peso forma perfetto, senza un filo di grasso; che probabilità abbiamo che sua una persona sportiva, oppure un tipo sedentario? potremmo stimare che, essendo in forma, sia un tipo sportivo con una probabilità, ad esempio, dell’80%.
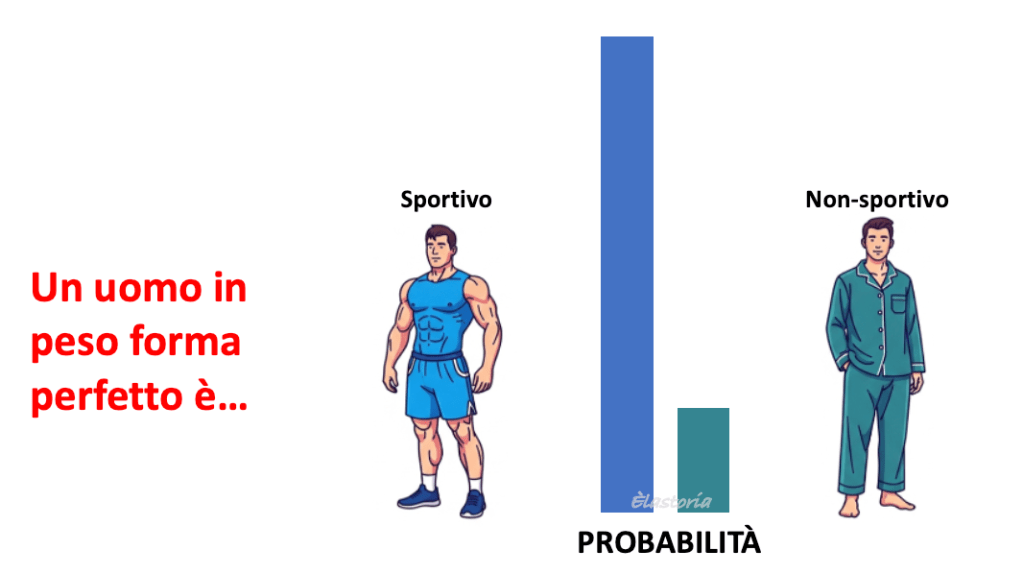
Poi, però, prendiamo ulteriori informazioni, e scopriamo che, nella città dove siamo, solo una persona su dieci è sportiva.
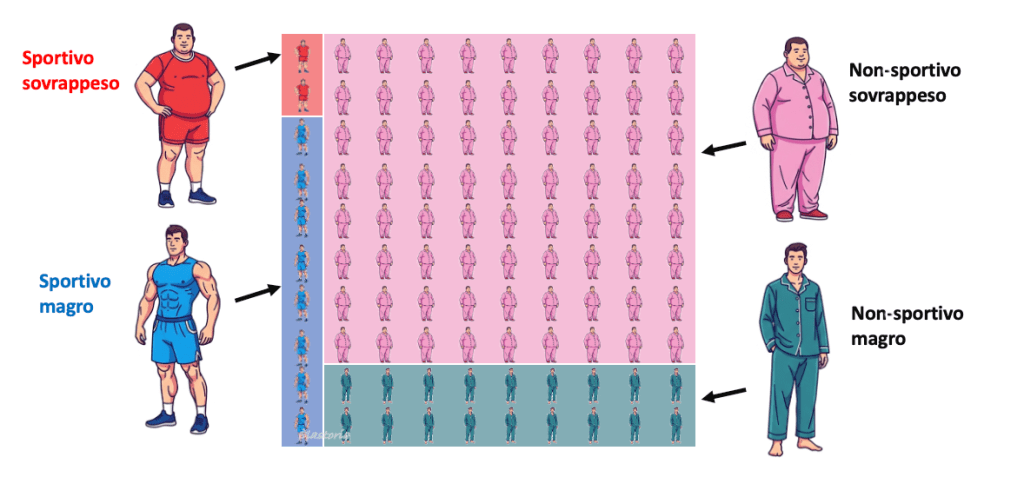
In base a questa nuova informazione, la nostra stima deve cambiare: le persone sedentarie sono molte di più, quindi tra loro ci saranno anche moltissimi magri. Il disegno qui sotto mostra tutte le possibili opzioni, e la loro frequenza nella popolazione (Nota personale: io mi colloco nel piccolo rettangolo rosso).
Sulla base di questo ragionamento allargato quindi è più probabile che il nostro uomo, pur essendo in forma, sia un non-sportivo, semplicemente perché i non-sportivi sono la maggioranza.
La formula di Bayes ci permette di definire questo ragionamento in maniera quantitativa:
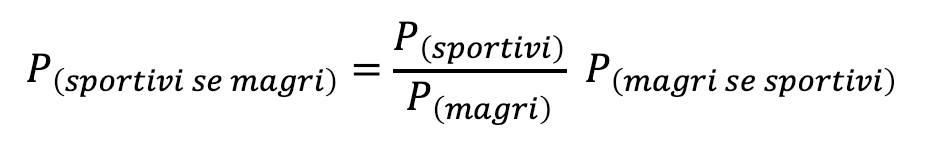
Inserendo i numeri del nostro grafico nella formula, otteniamo che una persona magra presa ha caso ha meno di una probabilità su tre di essere sportiva!!!
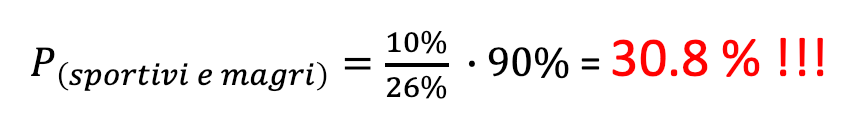
La formula generale del teorema di Bayes è:

Tradotta in Italiano, suonerebbe così:
La probabilità che A sia vero se B è vero è uguale alla probabilità assoluta di A, divisa per la probabilità assoluta di B, moltiplicate per la probabilità che B sia vero se A è vero.
Indovinello finale
Vi lascio con un indovinello che si può risolvere col teorema di Bayes, ma che è estremamente contro-intuitivo; quando fu pubblicato scatenò dibattiti e incredulità sulla sua soluzione.
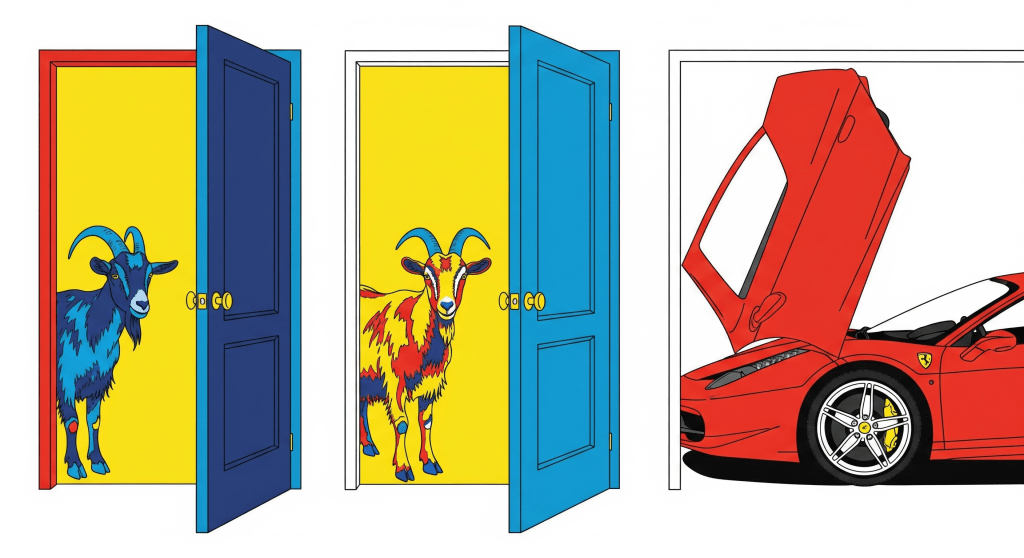
In un gioco in TV siete di fronte a tre porte e potete sceglierne solo una, vincendo quello che nasconde: due nascondono una capra, la terza una Ferrari. Scegliete una delle porte a caso, senza aprirla; dopo la vostra scelta, il presentatore decide di aiutarvi, e apre una delle altre due porte, mostrando una capra.
Rimangono quindi solo due porte; quella che avete scelto e l’altra. Il presentatore vuole ancora aiutarvi e vi offre la possibilità di cambiare la scelta iniziale. Cambiate porta o no?
Buon divertimento.

























































Lascia un commento